2022年蓝桥杯Python A组省赛做题记录

2025-03-01

ACM

11k words

A. 裁纸刀
B. 寻找整数
C. 质因数个数
D. 矩形拼接
E. 消除游戏
F. 重新排序
G. 全排列的价值
H. 最长不下降子序列
I. 最优清零方案
J. 数的拆分

做题进度，目前还剩：

[ ] H（30pts，还没de出bug）
[ ] J（还没做）

其他均已完成。

A. 裁纸刀

题目链接：https://www.lanqiao.cn/problems/2060/learning

经过观察可以发现不管怎么切，刀数都是一样的。因此直接给出答案：

def solve(n, m):
    return 4 + n * m - 1

n, m = 20, 22
print(solve(n, m))

B. 寻找整数

题目链接：https://www.lanqiao.cn/problems/2131/learning

也就是说给了一堆模的方程，求这个数最小值。

最朴素的暴力跑 $10^{17}$ （ $2^{60}$ 左右）三个小时肯定跑不完。最快的方法应该是逐步合并的CRT，但是这题通过简单优化暴力，也可以很快跑出来。

暴力的思路是，假设我们目前已经知道了一个同余方程

$n \equiv A (\mod M)$

那么现在 $n$ 最小肯定是 $A$ 。

现在新加入一个同余方程，要求 $n$ 也满足

$n\equiv r (\mod m)$

假设这个是一定能被满足的（题意，所以无需判断无解的情况），新的模数 $M'$ 很显然是 $\text{lcm} (M,m)$ 。那我们暴力以 $M$ 的步长，寻找下一个最小的同时满足前面两个方程的 $n'$ ，因为是最小的，也就是新的 $A'$ 。这样我们就得到了新的

$n\equiv A' (\mod M')$

然后这样跳个50次就得到了答案。不会分析这个时间复杂度，但是很显然就是能很快跑出来的，毕竟这个 $M$ 是一直在做lcm，指数级别增大的。

import math

def solve(data):
    n, step = data[0]
    for i in range(1, len(data)):
        m, r = data[i]
        while n % m != r:
            n += step
        step = (step * m) // math.gcd(step, m)
    return n

if __name__ == '__main__':
    data = [
        (2, 1), (3, 2), (4, 1), (5, 4), (6, 5), (7, 4), (8, 1), (9, 2),
        (10, 9), (11, 0), (12, 5), (13, 10), (14, 11), (15, 14), (16, 9),
        (17, 0), (18, 11), (19, 18), (20, 9), (21, 11), (22, 11), (23, 15),
        (24, 17), (25, 9), (26, 23), (27, 20), (28, 25), (29, 16), (30, 29),
        (31, 27), (32, 25), (33, 11), (34, 17), (35, 4), (36, 29), (37, 22),
        (38, 37), (39, 23), (40, 9), (41, 1), (42, 11), (43, 11), (44, 33),
        (45, 29), (46, 15), (47, 5), (48, 41), (49, 46)
    ]
    
    ans = solve(data)
    print(ans)

C. 质因数个数

题目链接：https://www.lanqiao.cn/problems/2155/learning

最大运行时间 10s， $n$ 最大 1e16， $O(\sqrt n)$ 的算法应该可以过。

一开始想手写一个筛法，筛 $\sqrt n$ 以内的所有质数即可。但是马上MLE了，1e8的set是存不下的应该，虽然算了下512MB可以存的下。然后直接分解质因数，对于质因数直接把全部因子都除掉，这样可以保证下一个能取模的数一定还是质数（更小的因子已经没了）。

# 90 %
import os
import sys

n = int(input())

ans = 0

x = 2
while x * x <= n:
    if n % x == 0:
        while n % x == 0:
            n = n // x
        ans += 1
    x += 1

if n != 1:
    ans += 1
print(ans)

这样写只有90分，还是T了一个点。需要继续优化，进一步的优化方案逐步如下。

① 必须注意Python中for .. range比while要快得多，因为for .. range遍历底层是由C语言实现的。

这样优化后，本地测试，运行速度从 9s 可以优化到 7s，那很好了。

import os
import sys

n = int(input())

ans = 0

import math
lim = math.floor(math.sqrt(n)) + 1
for x in range(2, lim):
    if x * x > n:
        break
    if n % x == 0:
        while n % x == 0:
            n = n // x
        ans += 1

if n != 1:
    ans += 1
print(ans)

但是蓝桥杯的古董机好像还不够，还是会T一个点。

② 发现是因为引入math库好像会慢一点点，去掉math库就好了。现在可以A了。但是看时间有点极限。

# 100 %

import os
import sys
import math

n = int(input())

ans = 0

for x in range(2, int(n**0.5)+1):
# lim = math.floor(math.sqrt(n)) + 1
# for x in range(2, lim):

    if x * x > n:
        break
    if n % x == 0:
        while n % x == 0:
            n = n // x
        ans += 1

if n != 1:
    ans += 1
print(ans)

③ 继续优化的话，就是对2特判，这样后面就只需要枚举奇数即可。下面是最后时间稳过的代码，本地运行从前面的9s、7s到3.5 s。

import os
import sys
import math

n = int(input())

ans = 0

if n % 2 == 0:
    while n % 2 == 0:
        n = n // 2
    ans += 1

for x in range(3, int(n**0.5)+1, 2):
    if x * x > n:
        break
    if n % x == 0:
        while n % x == 0:
            n = n // x
        ans += 1

if n != 1:
    ans += 1
print(ans)

D. 矩形拼接

题目链接：https://www.lanqiao.cn/problems/2154/learning

很容易想到是那种史山模拟题，有一大堆if else。只能试图比较有条理的枚举。

我的思路是，首先任意选两块拼一起，最坏情况就是随便乱放的时候，会有8条边。

一种一定能达到的更优情况，是两条边共线的情况：

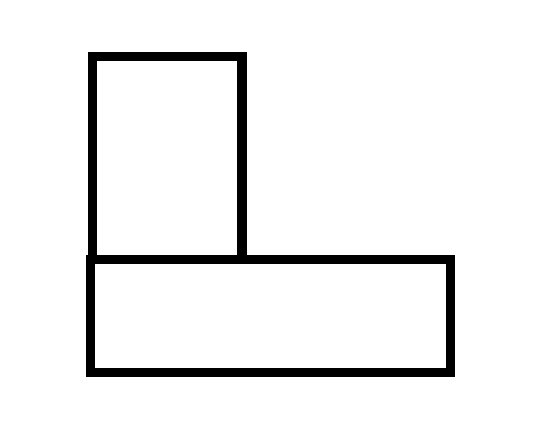
这种情况可以视为一个大矩形有一个缺口。

不妨在假设第三个矩形一定填在这个叠起来的（最多6边）形的某一个边上。这样就能直接枚举了。（我三个矩形枚举所有可能排列）。

这样，每个询问，搜索的次数是 $3!\times 2^3 \times 6=36\times 8$ ，最后的时间复杂度是可以接受的。

try:
    from debug_utils import debug
except:
    def debug(*args):
        pass

import os
import sys

def solve():
    a1, b1, a2, b2, a3, b3 = map(int, input().split())
    rects = [[a1, b1], [a2, b2], [a3, b3]]
    ans = 8
    for base in rects:
        for s in range(2):
            down, near = base[s], base[1-s]
            for above in rects:
                if base is above:
                    continue
                for t in range(2):
                    up, left = above[t], above[1-t]
                    if up > down:
                        continue
                    """
                               up
                             |----|
                    left     |    |
                             |---------|
                    near     |         |
                             ----------|
                                down
                    """
                    if down != up:
                        angles = [down - up, left, up, left + near, down, near]
                    else:
                        angles = [up, left + near, down, left + near]
                    for rect in rects:
                        if rect is not base and rect is not above:
                            for u in range(2):
                                a, b = rect[u], rect[1-u]
                                """
                                    a
                                    |------|
                                b   |      |
                                    --------
                                """
                                normal = len(angles) + 2
                                now = normal
                                if len(angles) == 6:    # 存在270度角
                                    now = min(now, normal - ((2 if a == angles[0] else 0) + (2 if b == angles[1] else 0)) )
                                # 普通处理90度
                                for idx in range(len(angles)):
                                    if len(angles) == 6 and idx <= 1:
                                        continue
                                    c = angles[idx]
                                    now = min(now, normal - (2 if c == a else 0))
                                ans = min(now, ans)
    print(ans)


t = int(input())
for _ in range(t):
    solve()

E. 消除游戏

题目链接：https://www.lanqiao.cn/problems/2127/learning

纯模拟题，感觉最简单的写法就是直接 $O(n)$ 模拟一个链表，初始遍历一遍找到可以删的节点，然后每次删除时把这个节点左边、右边、左边的左边、右边的右边，4个节点都纳入考虑范围。（然后就和下面的代码一样模拟成构思了，写了快一百多行）

import os
import sys

class Node:
    __slots__ = ('val', 'prev', 'next', 'alive')
    def __init__(self, val, prev = None, next = None):
        self.val = val
        self.prev = prev
        self.next = next
        self.alive = True
    def __repr__(self):
        return str(self.val)

class Linklist:
    def __init__(self):
        self.head = Node(None)  # 哨兵头尾
        self.tail = Node(None)
        self.head.next = self.tail
        self.tail.prev = self.head
    def insert(self, val, node = None):
        if node == None:
            node = self.tail.prev
        one = Node(val, node, node.next)
        node.next = one
        one.next.prev = one
        return one
    def remove(self, node):
        node.prev.next = node.next
        node.next.prev = node.prev
        node.alive = False
        
    def __repr__(self):
        line = []
        now = self.head.next
        while now is not self.tail:
            line.append(now.val)
            now = now.next
        ret = ''.join(line)
        return ret if ret != '' else 'EMPTY'


def solve():
    lines = sys.stdin.read().splitlines()

    s = lines[0]
    if s == '':
        print("EMPTY")
        return 

    n = len(s)

    lst = Linklist()
    que = []

    for i in range(n):
        ptr = lst.insert(s[i])
        if  (0 < i < n-1 and ( (s[i-1] == s[i] != s[i+1]) or (s[i-1] != s[i] == s[i+1]) ) ) or \
            (0 <= i and i+2 < n and s[i] != s[i+1] == s[i+2]) or \
            (i - 2 >= 0 and i < n and s[i-2] == s[i-1] != s[i]):
            que.append(ptr)
            ptr.alive = False
    
    while len(que) != 0:
        wait = []
        for p in que:
            lst.remove(p)
            if p.prev.val is not None and p.prev.alive:
                wait.append(p.prev)
            if p.prev.prev is not None and p.prev.prev.val is not None and p.prev.prev.alive:
                wait.append(p.prev.prev)
            if p.next.val is not None and p.next.alive:
                wait.append(p.next)
            if p.next.next is not None and p.next.next.val is not None and p.next.next.alive:
                wait.append(p.next.next)
        new_que = []
        for p in wait:
            if p.alive == True and \
                ((((p.prev.val == p.val != p.next.val and p.next.val is not None) or (p.prev.val != p.val == p.next.val and p.prev.val is not None)) ) or \
            (p.next.next is not None and p.val != p.next.val == p.next.next.val) or \
            (p.prev.prev is not None and p.prev.prev.val == p.prev.val != p.val)):
                new_que.append(p)
                p.alive = False
        que = new_que
    print(lst)

solve()

F. 重新排序

题目链接：https://www.lanqiao.cn/problems/2128/learning

（感觉是这场最简单的一题。）

第 $i$ 个元素，对最终和的贡献，取决于它处于几个区间内。如果处于 $c_i$ 个区间内，那最终贡献就是 $a_i \cdot c_i$

我们可以 $O(N)$ 预处理出来第 $i$ 个位置处于区间个数的 $c_i$ 。（这种区间叠加，直接用差分即可）

对于越大的 $c_i$ ，很显然匹配越大的 $a_i$ ，会使得结果最大。

import os
import sys

lines = sys.stdin.read().splitlines()

n = int(lines[0].strip())
a = list(map(int, lines[1].split()))
m = int(lines[2].strip())
cnt = [0] * (n)
for i in range(m):
    l, r = map(int, lines[i+3].split())
    l -= 1
    r -= 1
    cnt[l] += 1
    if r+1 < n:
        cnt[r+1] -= 1
for i in range(1, n):
    cnt[i] += cnt[i-1]

ans = 0
for i in range(n):
    ans -= cnt[i] * a[i]

cnt = sorted(cnt)
a = sorted(a)
for i in range(n):
    ans += cnt[i] * a[i]
print(ans)

G. 全排列的价值

题目链接：https://www.lanqiao.cn/problems/2137/learning

和前面一题一样，从贡献的角度切入。数 $i$ ，在排列中对这个排列价值的贡献就是它后面所有比它大的数的个数。全排列中，对于数 $j$ （ $j>i$ ），会有多少次机会也就是有多少个排列，会排在 $i$ 后面？很显然是 $(n-2)!\cdot (C_{n-1}^2+n-1)$

也就是说所，数 $i$ 对最后我们要输出的答案的贡献是

$\begin{aligned} ans[i]&=\bigl( \sum_{j=i+1}^n (n-2)!\cdot (C_{n-1}^2+n-1) \bigr)\\ &= (n-2)!\cdot (C_{n-1}^2+n-1) \cdot (n-i)\\ \end{aligned}$

最后总的答案是

$\begin{aligned} ans &= (n-2)!\cdot (C_{n-1}^2+n-1)\cdot \frac 1 2 n (n-1)\\ &= \frac 1 4 n!\cdot n(n-1) \end{aligned}$

然后需要注意，如果不写逆元，就需要特判一下两个 2 因子消掉即可。

import os
import sys
import math

n = int(input())
m = 998244353

def fac_2(x):
    ret = 1
    for i in range(3, x + 1):
        ret *= i
        ret %= m
    return ret

ans = fac_2(n)
ans = (ans * (n * (n - 1) // 2 % m)) % m

print(ans)

H. 最长不下降子序列

链接：https://www.lanqiao.cn/problems/2088/learning

I. 最优清零方案

链接：https://www.lanqiao.cn/problems/2138/learning

很显然可以发现，我们只要先尽可能地 $k$ 个连续消掉，随便做，消到没办法再消，然后对剩下的逐个消除即可。

因此直接 $O(n)$ 遍历一遍，遍历到 $i$ 时，对 $[i, i+k-1]$ 消掉 $\min_{j\in [i,i+k-1]}{a_j}$ 即可。正确性是有保证的。

下面是暴力的写法，时间复杂度最坏 $O(nk)$ .

import os
import sys

n, k = map(int, input().split())
a = list(map(int, input().split()))

ok = -1
ans = 0
for i in range(n):
    if i <= ok or i+k > n:
        ans += a[i]
    else:
        j = i
        for p in range(i, i+k):
            if a[p] < a[j]:
                j = p
        h = a[j]
        ans += h
        for p in range(i, i+k):
            a[p] -= h
        ans += a[i]
        ok = j
print(ans)

虽然这题时间复杂度非常坏，最坏会到 $O(nk)$ ，但是蓝桥杯官网上测试这段代码，是直接100%通过……

但是还是看下怎么优化。

上述的步骤，说简单就是对于 $i$ ，我们对 $[i,i+k)$ 这一个区间，全部减去区间中最小的 $a[j]$ ，然后 $i$ 就可以跳到 $j$ 了，继续下一步即可，可以看出主要的时间复杂度的问题都在寻找这个最小的 $a[j]$ 上和区间减法上了，因为朴素的做法中，一定要遍历 $k$ 个数才能找到最小的，在不打标记的情况下，区间减法也是要一个个减掉的。所以很自然会想到用线段树来实现区间减法和最小值寻找，这样时间复杂度就变成了 $O(n\log n)$ ，对的。

除此之外我感觉也可以用双端队列来做。但是写起来可能比线段树更难调，那不如直接线段树了。但是线段树会狠狠卡常，必须尽可能不搜就不搜。

import sys

n, k = map(int, sys.stdin.readline().split())
a = list(map(int, sys.stdin.readline().split()))
inf = 2e9
ans = sum(a)

class SegmentTree:
    def __init__(self, data):
        self.n = len(data)
        self.tree = [[0, 0] for _ in range(4 * self.n)] 
        self.lazy = [0] * (4 * self.n)
        self._build(0, 0, self.n-1, data)
        
    def _build(self, u, l, r, data):
        if l == r:
            self.tree[u] = [data[l], l]
        else:
            mid = (l + r) // 2
            self._build(2*u+1, l, mid, data)
            self._build(2*u+2, mid+1, r, data)
            left_val, left_idx = self.tree[2*u+1]
            right_val, right_idx = self.tree[2*u+2]
            if left_val < right_val:
                self.tree[u] = [left_val, left_idx]
            else:
                self.tree[u] = [right_val, right_idx]

    def _query(self, u, l, r, L, R):
        if R < l or r < L:
            return [inf, -1] 
        if L <= l and r <= R:
            return self.tree[u]
        self._push(u)
        mid = (l + r) // 2
        left = self._query(2*u+1, l, mid, L, R)
        right = self._query(2*u+2, mid+1, r, L, R)
        return left if left[0] < right[0] else right

    def find_min(self, l, r):
        return self._query(0, 0, self.n-1, l, r)

    def _push(self, u):
        if self.lazy[u] != 0:
            self.tree[2*u+1][0] += self.lazy[u]
            self.lazy[2*u+1] += self.lazy[u]
            self.tree[2*u+2][0] += self.lazy[u]
            self.lazy[2*u+2] += self.lazy[u]
            self.lazy[u] = 0

    def _range_add(self, u, l, r, L, R, x):
        if R < l or r < L:
            return
        if L <= l and r <= R:
            self.tree[u][0] += x
            self.lazy[u] += x
            return
        self._push(u)
        mid = (l + r) // 2
        self._range_add(2*u+1, l, mid, L, R, x)
        self._range_add(2*u+2, mid+1, r, L, R, x)
        left_val, left_idx = self.tree[2*u+1]
        right_val, right_idx = self.tree[2*u+2]
        if left_val < right_val:
            self.tree[u] = [left_val, left_idx]
        else:
            self.tree[u] = [right_val, right_idx]

    def range_sub(self, l, r, x):
        self._range_add(0, 0, self.n-1, l, r, -x)

    def range_sum(self, u, l, r):
        if l == r:
            return self.tree[u][0] 
        self._push(u)
        mid = (l + r) // 2
        return self.range_sum(2*u+1, l, mid) + self.range_sum(2*u+2, mid+1, r)

segtree = SegmentTree(a)
p = -1
for i in range(n):
    if i + k <= n and i > p:
        min_val, min_idx = segtree.find_min(i, i + k - 1)
        segtree.range_sub(i, i + k - 1, min_val)
        p = min_idx
        ans -= k * min_val
        ans += min_val
print(ans)

J. 数的拆分

链接：https://www.lanqiao.cn/problems/2090

Categories

Tags