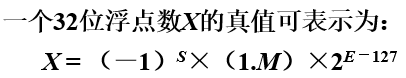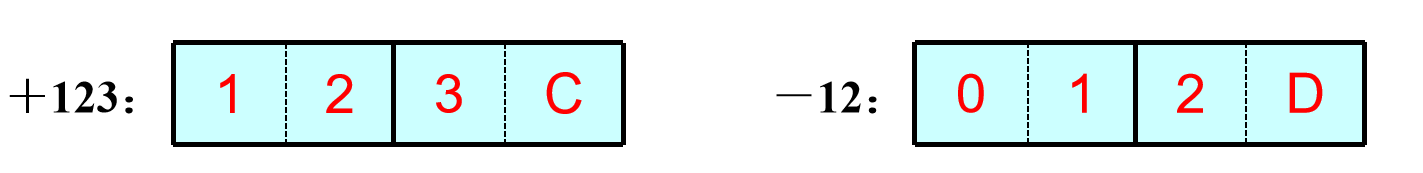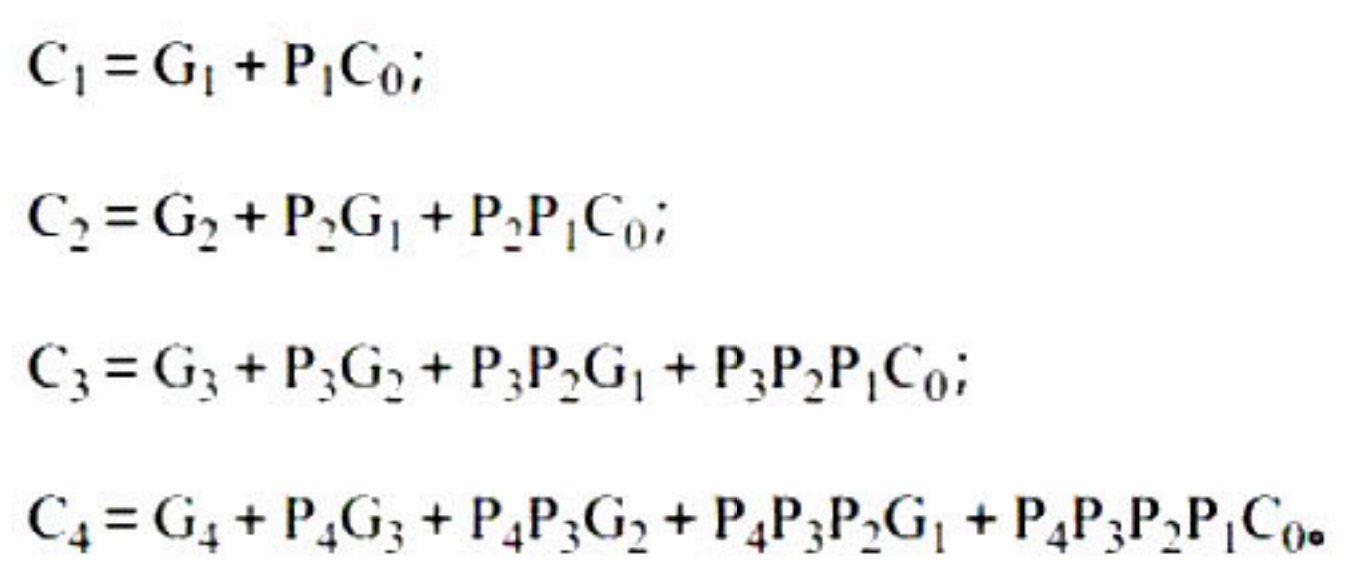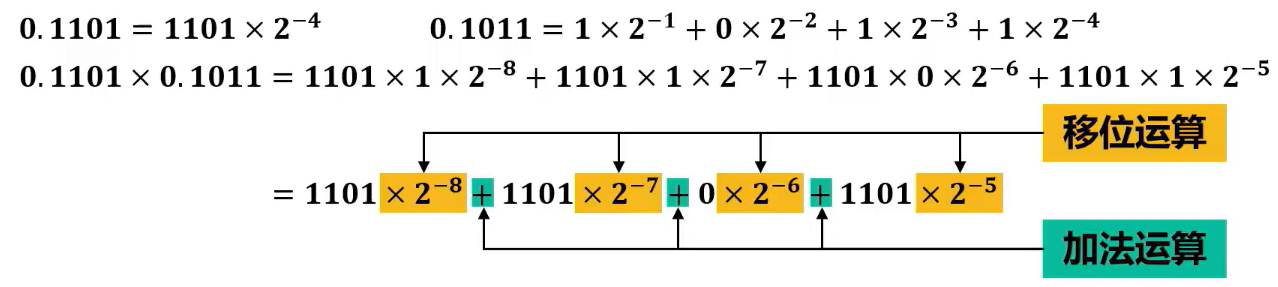计算机组成原理笔记（1） 运算方法与运算器

课程笔记
7.7k words

定点数

定点数是指小数点的位置固定不变。小数点的位置是事先约定的，不需要占用一个二进制位来表示。通常将数据表示成纯小数或纯整数。

定点整数

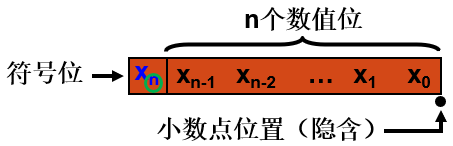
image-20240909003523919

也就是小数点在最后面，原码表示时，范围是：0≤∣X∣≤2n−10\leq|X|\leq 2^n-1

定点小数

小数点位于符号位和最高有效位之间。

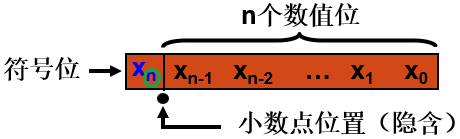
image-20240909003629643

表示范围是：0≤∣X∣≤1−2−n0\leq |X|\leq 1-2^{-n}

原码、补码、反码、移码

略。

移码等于补码的符号位取反；移码的大小关系与真值的大小关系相同。

浮点数

一个 RR 进制的数 NN 可以写成

N=M×REN=M\times R^E

其中 MM 为尾数，EE 为指数，RR 为基数（通常取2、8、16）。

image-20240909010643395

浮点数的规格化

单纯这样写的话，同一个小数，浮点表示方法不是唯一的。为让表示形式唯一，规定，当尾数 MM 不为0的时候：

① 若尾数用原码表示，规定

12≤∣M∣<1\frac{1}{2}\leq |M|<1

也就是说，尾数的二进制形式为 0.1××...0.1\times \times ...（正的）或 1.1××...×1.1\times\times ...\times（负的，最前面小数点前的是符号位）

② 若尾数用补码表示，规定

12≤M<1或−1≤M<−12\frac 1 2 \leq M<1或-1\le M<-\frac 1 2

也就是说，尾数的二进制形式为 0.1××...0.1\times \times ...（正的）或 1.0××...×1.0\times\times ...\times，这样能保证浮点数尽可能地精确。

M=−12M=-\frac 1 2 对于原码来说是规格化的，对于补码则不是。

当浮点数的尾码 M=0M=0，不管阶码是什么，都是视为零，这是机器零。要求这时候机器把浮点数的阶码和尾数都清零，保证零的唯一性。

设阶码和尾数都用补码表示，阶码共 k+1k+1 位（含一位阶符），尾数共 n+1n+1 位（含一位数符），表示范围是

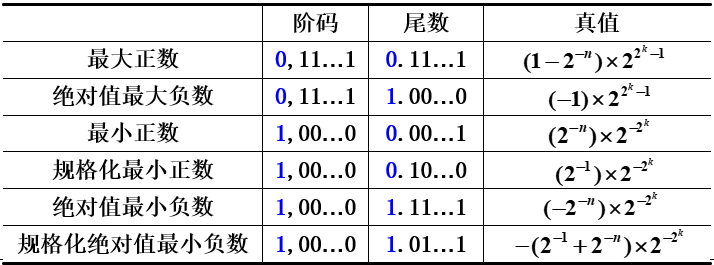
image-20240909011710757

IEEE754标准

image-20240909011803795

image-20240909011825098

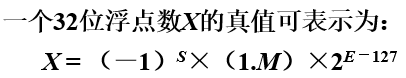
image-20240909011834230

image-20240909011901030

image-20240909011918902

十进制数串的表示方法

一般有两种方法：

① 字符串。一个字节存放一个十进制数或符号的ASCII码。用于非数值计算领域/

② 压缩的十进制数串。每个字节存放两个十进制数位，每个数位占4位二进制数。通常存放该十进制数位的8421码。符号位也占半个字节，并存放在最低数值位之后，通常用1100表示正号，1101表示负号。在这种表示中，规定数字的个数加符号位之和必须为偶数；当和为奇数时，应在最高数值位之前补0。

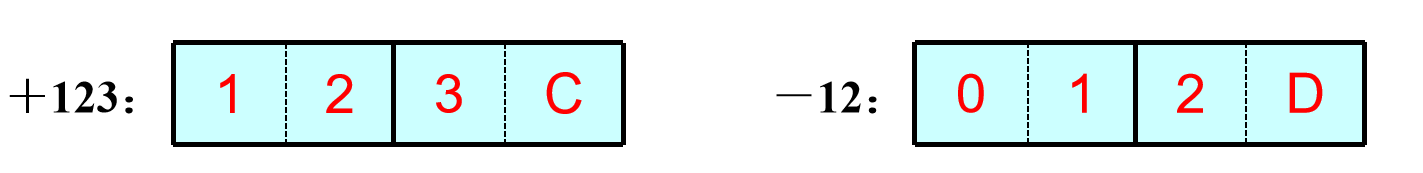
image-20240913012530887

例题

image-20240912163037607

（1）

X=256.5=(+100000000.1)2=+(0.1000000001×29)2\begin{aligned} X=256.5&=(+100000000.1)_2=+(0.1000000001\times 2^{9})_2\\ \end{aligned}

因此阶码为：(9)补=0000 1001(9)_补=0000\space1001

尾数为：(+0.1000000001)补=0.100 0000 0010 0000 0000 0000(+0.1000000001)_补=0.100\space 0000\space 0010 \space 0000\space 0000\space 0000

用十六进制表示：

(09402000)16(09402000)_{16}

（2）

同理的。

X=−256.5=(−100000000.1)2=(−0.1000000001×29)2\begin{aligned} X=-256.5&=(-100000000.1)_2=(-0.1000000001\times 2^{9})_2\\ \end{aligned}

阶码为：(9)补=0000 1001(9)_补=0000\space1001

尾数为：(−0.1000000001)补=1.011 1111 1110 0000 0000 0000(-0.1000000001)_补=1.011\space 1111\space 1110 \space 0000\space 0000\space 0000

用十六进制表示：

(09BFE000)16(09BFE000)_{16}

image-20240912170302452

数据表示

ASCII码

ASCII码是128个字符组成的字符集。其中编码值0～31和127为控制字符，用于通信中的通信控制或对计算机设备的功能控制。另外95个编码对应于95个可以从计算机终端输入并且可以显示和打印的有形字符。

一个字符在计算机中占据一个字节，用8位二进制数表示。其中最高位b7在传输过程中可用作奇偶校验位，存储字符时则取0。

规律：

① 字符0～9这10个数字符的高3位编码为011，低4位为0000～1001。当去掉高3位的值时，低4位正好是二进制形式的0～9。

② 英文字母的编码值满足正常的字母排序关系，且大小写英文字母编码的对应关系相当简便，差别仅表现在b5一位的值为0或1，

校验码

计算机内常遇到的错误有两大类：随机错误和突发错误。前者是孤立出现的一个错误，后者是连续产生的一批错误。本节只讨论前者。

奇偶校验码

奇校验：

P=Dn−1⊕...⊕D1⊕D0‾P=\overline {D_{n-1}\oplus ...\oplus D_1\oplus D_0}\\

偶校验：

P=Dn−1⊕...⊕D1⊕D0P=D_{n-1}\oplus ...\oplus D_1\oplus D_0

奇偶校验码的码距为2，具有发现一位错误的能力。

定点加减运算

补码可以用来表示加法，减法就是相反数加法。

因为假设一个负数的补码，记录为真实值，真实值表示的实际上就是在模 2n+12^{n+1} 下该负数的同余。所以符号位也是加入运算的。

例如，以4位有符号二进制数为例，十进制下4+(−3)4+(-3)

\begin{array}{c@{}c@{}c@{}c@{}c} & 0 & 1 & 0 & 0 \\ + & 1 & 1 & 0 & 1 \\ \hline & \color{red}{0} & \color{red}{0} & 0 & 1 \\ \end{array}

这里红色的结果是带了进位的。

十进制下 (−4)+(−3)(-4)+(-3)

\begin{array}{c@{}c@{}c@{}c@{}c} & 1 & 1 & 0 & 0 \\ + & 1 & 1 & 0 & 1 \\ \hline & \color{red}{1} & \color{red}{0} & 0 & 1 \\ \end{array}

可以看出，负数相加，因为补码的符号位参与运算，所以只有最高有效位产生了进位，才能保持这还是一个负数。

溢出检测

单符号位法

首先，一个没有溢出的正数，和一个没有溢出的负数，相加后必定不会溢出。

那么溢出的情况就是两种：

① 两个正数相加，最高有效位产生进位，导致符号位从0变为1，则产生正(上)溢。

② 两个负数相加，最高有效位没有提供进位，而符号位天然有进位（负数符号位都是1，此时相加，符号位从1变成0）则产生负(下)溢。

例如，十进制下 (−4)+(−5)(-4)+(-5)

\begin{array}{c@{}c@{}c@{}c@{}c} & 1 & 1 & 0 & 0 \\ + & 1 & 0 & 1 & 1 \\ \hline & \color{red}{0} & 1 & 1 & 1 \\ \end{array}

也就是说，如果不溢出，要求符号位有进位时，最高有效位也应该有进位；符号位没有进位时，最高有效位也应该没有进位。

溢出的逻辑表达式：

V=Ct⊕C0V=C_t\oplus C_0

其中 CtC_t 为符号位产生的进位，C0C_0 为最高有效位产生的进位。

双符号位法（变形补码）

一般来说，计算机中最常用的是模 2n+12^{n+1} 补码。但是溢出判断时可以采用双符号位法，也就是变形补码，可以让增加一倍表示的数的范围。

[x]_补=2^{n+2}+x & (\mod 2^{n+2}) \\

变形补码中，任何正数，两个符号位都是0，任何负数，两个符号位都是1。其他情况都是溢出了。溢出的逻辑表达式：

V=Sf1⊕Sf2V=S_{f1}\oplus S_{f2}

P31， 例18，19

加法器

计算机通过补码，把加减都变成了补码的加法，只需要实现加法器。

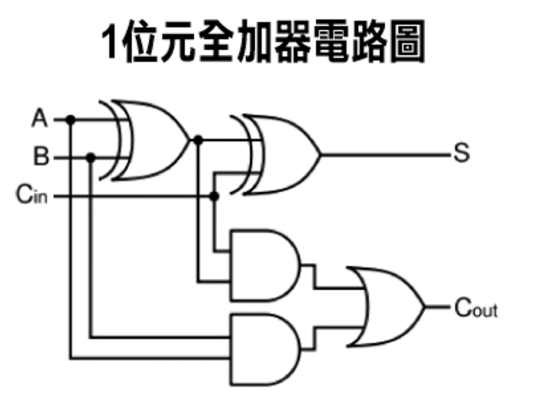
全加器

和数电中说的一样，输入 A,BA,B 和进位 CC，输出和 SS 和进位输出 C′C'。

S=A⊕B⊕CC′=AB+(A⊕B)CS=A\oplus B\oplus C\\ C'=AB+(A\oplus B)C

image-20240916022826592

进位方式

串行进位

从最低位开始逐位相加，产生的进位逐次向高位传递。

每一位的结果必须等到低位运算完成后才能建立起来，运算速度慢。

位数越多，速度越慢。

可以通过多个全加器级联实现。

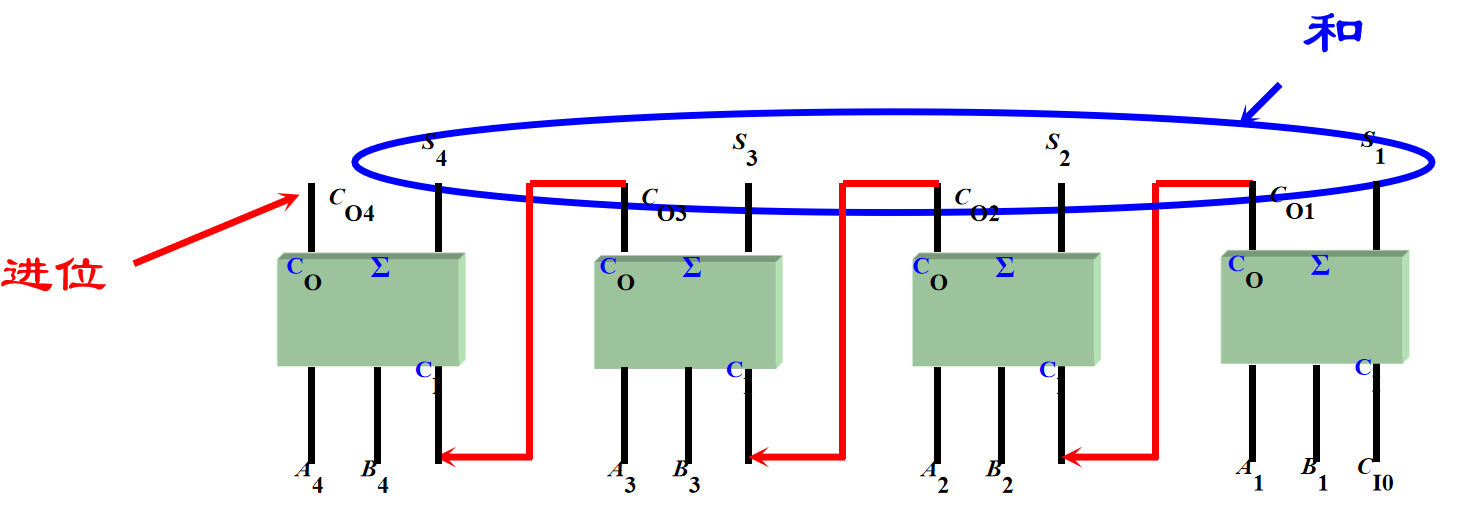
image-20240916021051714

这里有一个比较糟糕的问题是，例如我们要进行一个32位的数的加法，那就要等待32个全加器慢慢加完，不太优。所以引入了超前进位。

超前进位

从全加器看出来，这几个都有一个公共的东西，归纳一下：

G=AB & (生成函数)\\ P=A\oplus B & (传播函数)\\

这里的生成函数，意思是当两个位都为1时，该位会直接生成一个进位。传播函数则是，如果该位至少有一个1，那么可能会传播一个进位。

得到

S=P⊕CC′=G+PCS=P\oplus C\\ C'=G+PC

推导

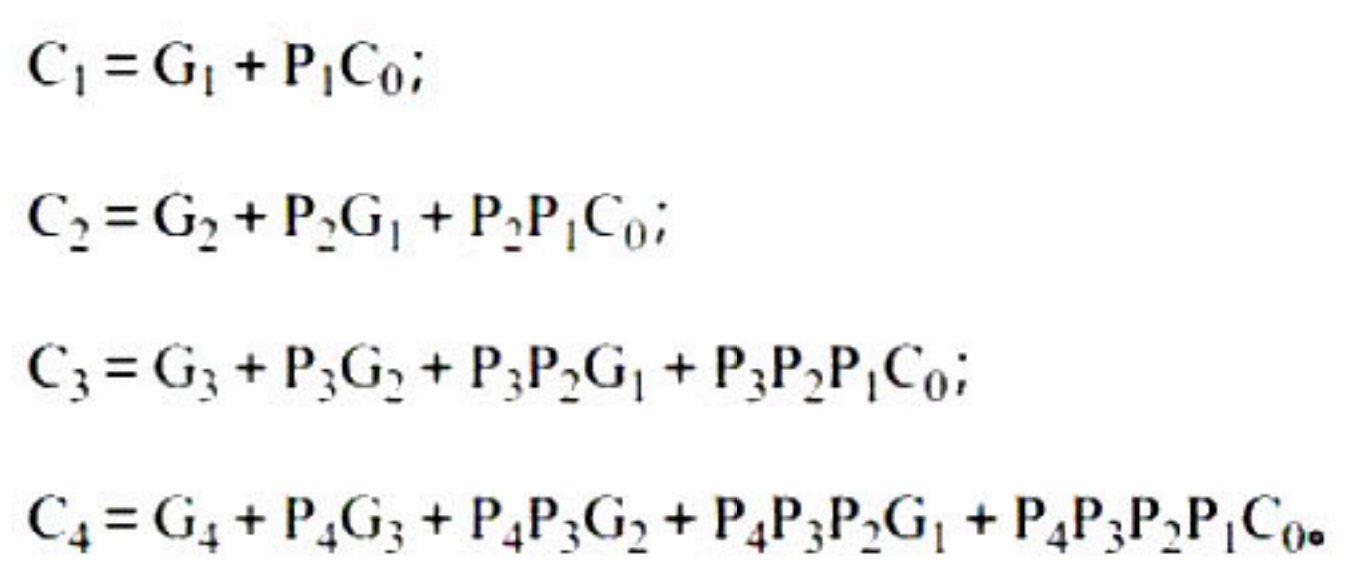
image-20240916025030989

定点乘除计算

定点乘法

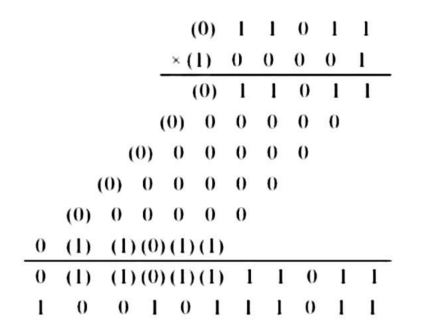
朴素的算法就是竖式计算

image-20240916204457914

实际上就是被乘数 0.1101 不断地乘以 1 或 0 的幂次，是移位运算与加法运算的叠加。

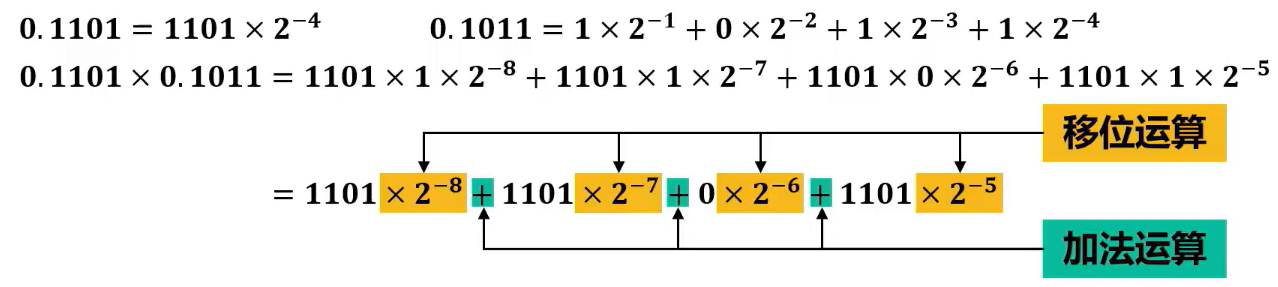
image-20240916170754001

这看上去比较简单，但是实际机器运行比较麻烦。除了需要大量加法器和移位器以外， nn 位二进制数的乘法，在竖式计算中需要把 nn 个比特同时加起来，普通的只有两数相加的加法器实现不了；并且需要两倍的寄存器。

可以进行优化，变成不断右移加上部分积。

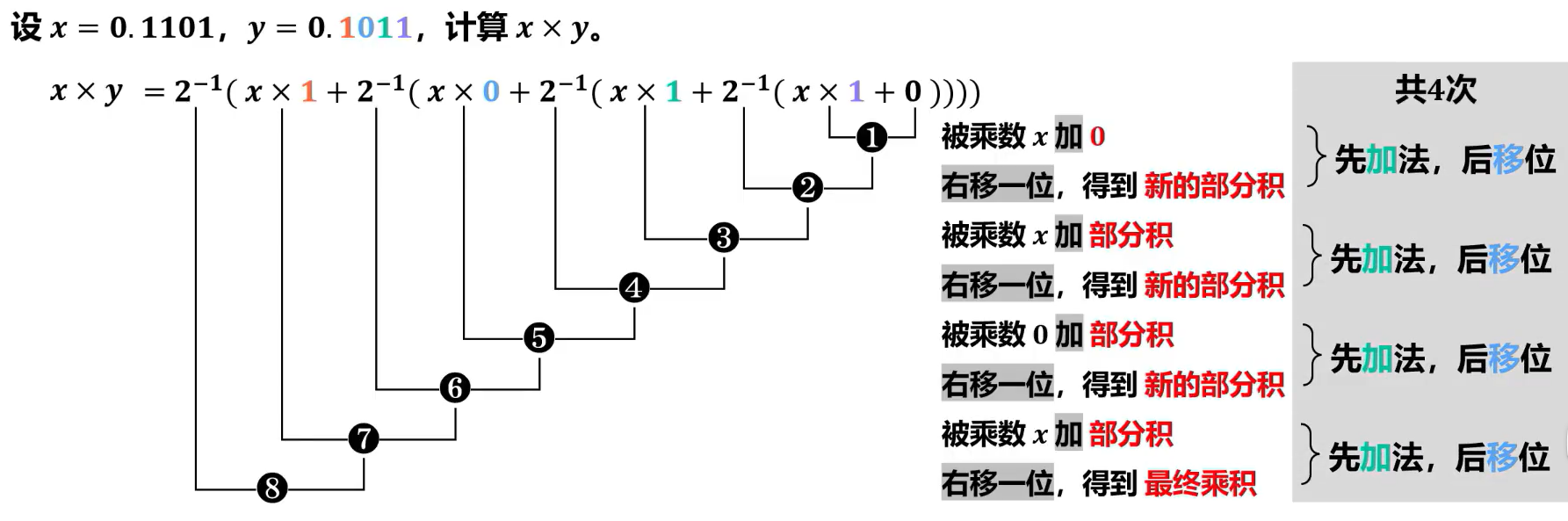
image-20240916171133626

这样就只需要一倍的寄存器了。

原码乘法

原码乘法就是单独对符号位做处理，然后直接乘就可以。

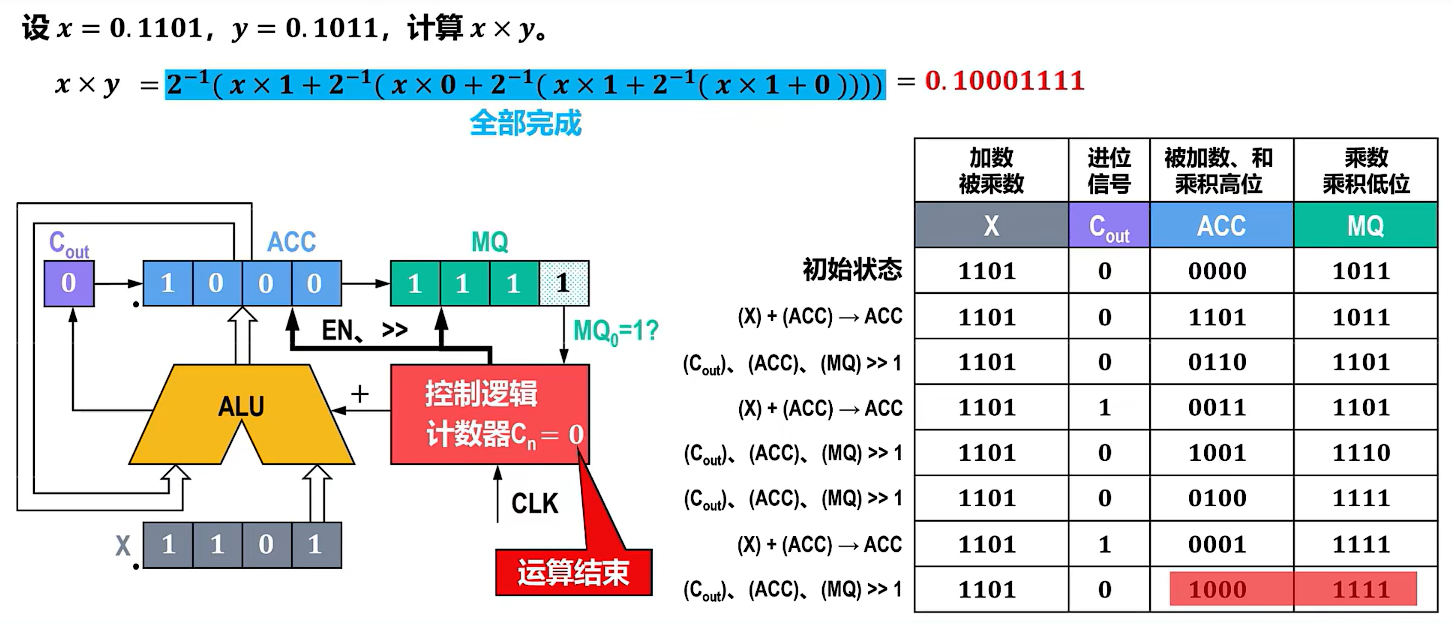
image-20240916201642424

补码乘法

由于计算机中用补码表示数据，如果用原码乘法计算两个数的乘积，运算前后需要进行补码->原码->补码的转换，比较麻烦，因此考虑引入Booth算法进行补码乘法。

略。

不带符号的阵列乘法器

湖科大教书匠 - 3-3-4 定点数的乘法运算

前面的算法，通过大量加法器、移位器，在时钟节拍下，进行多轮次的逻辑控制，速度比较慢。为了提升速度，可以采用组合逻辑电路，构成专用的阵列乘法器。

回想一下二进制乘法的竖式计算方法：

image-20240916202738793

能不能用组合逻辑电路实现上述运算？

显然是可以的，乘法运算是可以直接用与门实现的，现在我们只需要做列的加法，阵列的加法用一堆全加器。

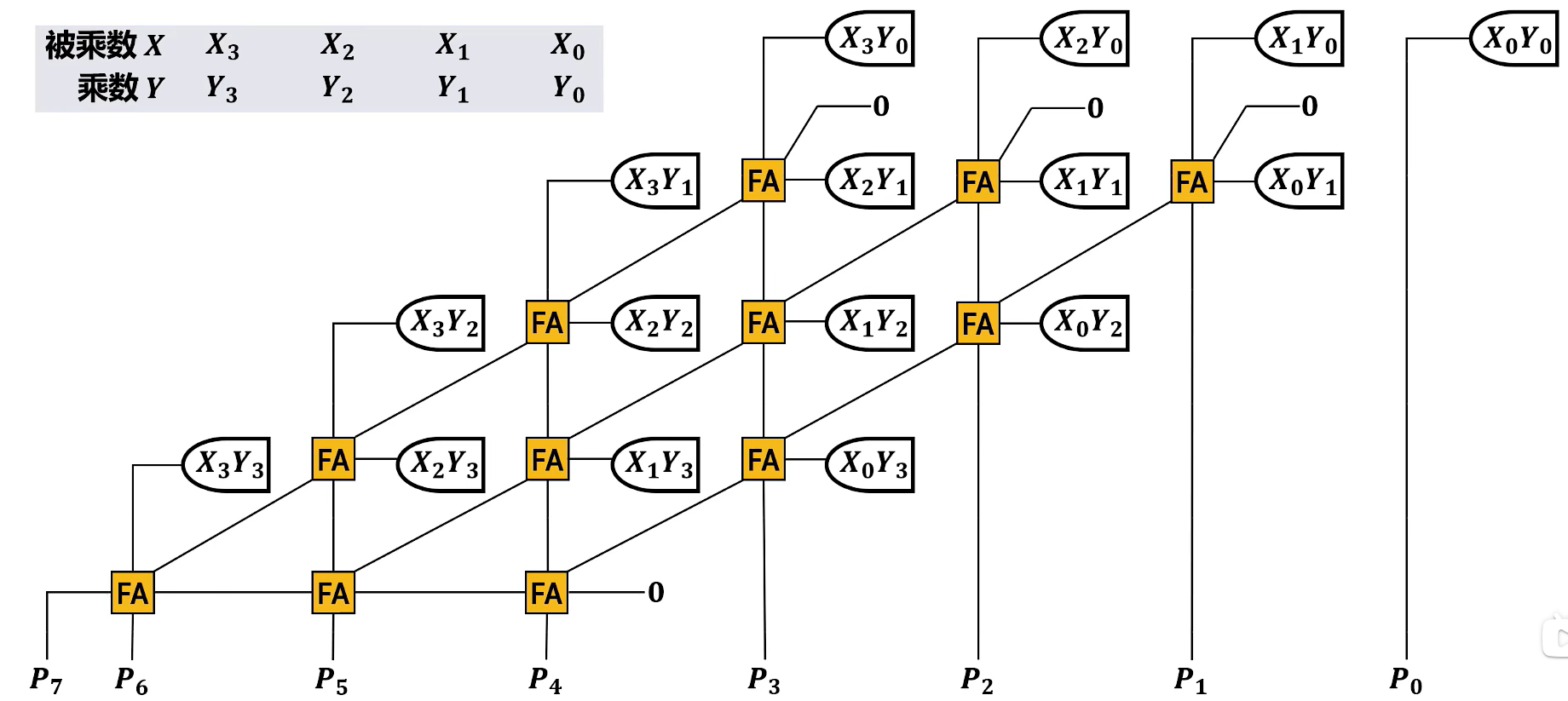
image-20240916202953635

上述的阵列乘法，用 n×(n−1)n\times (n-1) 个全加器 与 n2n^2 个与门构成。

与门是并行的，需要 1T1T 时延。各行行内的全加器不存在进位依赖，但是第ii 行的全加器依赖上一行全加器的进位，所以 4 位的阵列乘法器，全加器时间延迟是 6T6T

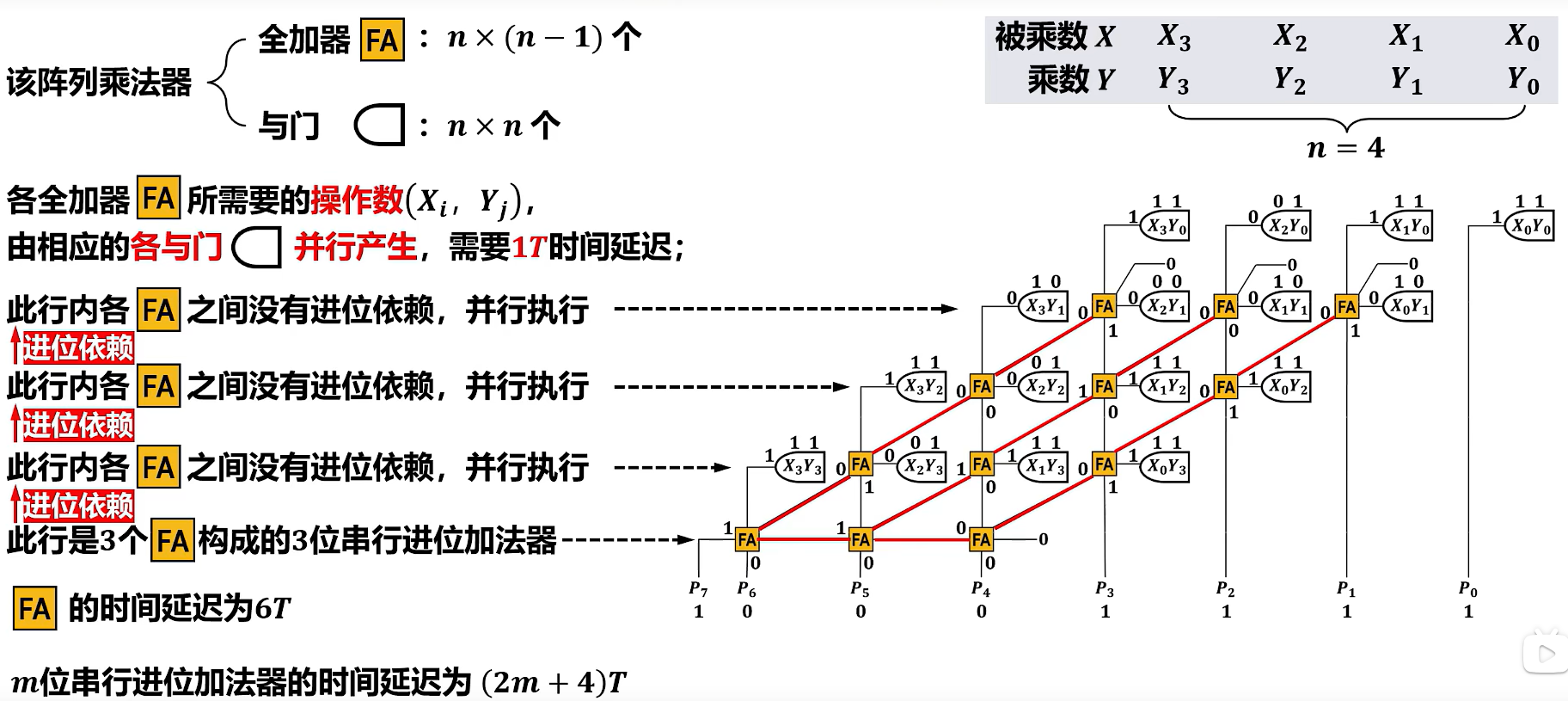
image-20240916204045090

得到这个阵列乘法器的时延是

1T+3×6T+(2×3+4)T=29T1T+3\times 6T+(2\times 3+4)T=29T

并且一开始有零输入的全加器，可以改成半加器，降低时延。最后的串行进位可以改成先行进位电路。

（课本上的理论推导）

设两个不带符号的二进制数

A=am−1...a1a0B=bn−1...b1b0A=a_{m-1}...a_1a_0\\ B=b_{n-1}...b_1b_0

数值分别是 aa 和 bb，即

a=∑i=0m−1ai2ib=∑j=0n−1bj2ja=\sum_{i=0}^{m-1}a_i 2^i\\ b=\sum_{j=0}^{n-1}b_j2^j

乘积

P=ab=(∑i=0m−1ai2i)(∑j=0n−1bj2j)P=ab=\left( \sum_{i=0}^{m-1}a_i 2^i \right)\left( \sum_{j=0}^{n-1}b_j2^j \right)

这就是一个阵列乘积，

P=ab=(∑i=0m−1ai2i)(∑j=0n−1bj2j)=∑i=0m−1∑j=0n−1(aibj)2i+j=∑k=0m+n−1pk2k\begin{aligned} P=ab&=\left( \sum_{i=0}^{m-1}a_i 2^i \right)\left( \sum_{j=0}^{n-1}b_j2^j \right)\\ &=\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}(a_ib_j)2^{i+j}\\ &=\sum_{k=0}^{m+n-1}p_k 2^k \end{aligned}

补码阵列乘法器

带求补器

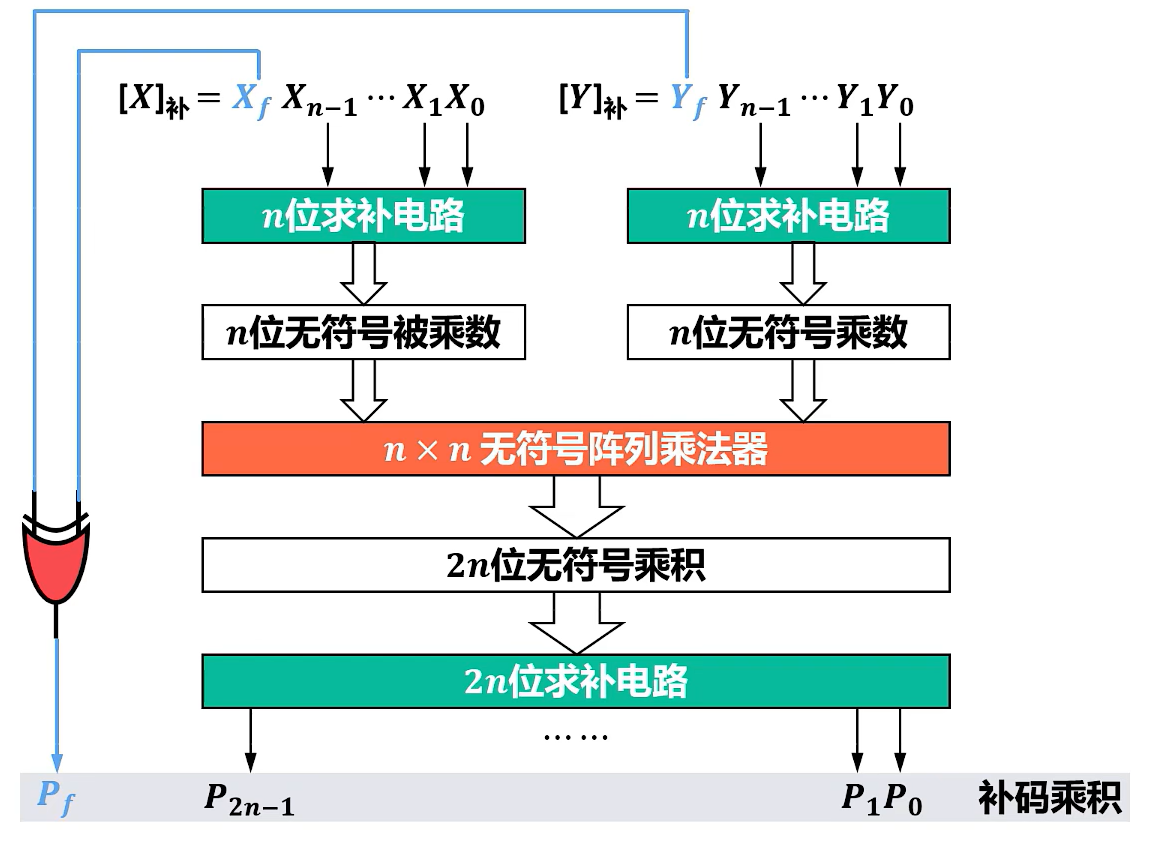
image-20240916210858273

直接补码阵列

直接补码乘法电路

设两个5位的二进制补码数

A=(a4)a3a2a1a0B=(b4)b3b2b1b0A=(a_4)a_3a_2a_1a_0\\ B=(b_4)b_3b_2b_1b_0

补码和真实值什么关系？从补码的意义我们知道，补码和真实值在 mod  2n+1\mod 2^{n+1} 的情况下是同余的。

[A]真≡[A]补mod  25[A]_{真} \equiv[A]_补 \mod 2^5\\

也就是说，如果已经知道真实值是负数，那直接补码表示的无符号数值减去 252^5 就是真实值（负数）。

[A]补=a0×20+a1×21+a2×22+a3×23+a4×24[A]真={a0×20+a1×21+a2×22+a3×23+a4×24−25ifa4=1a0×20+a1×21+a2×22+a3×23+a4×24other.(a4=0)[A]_补=a_0\times 2^0+a_1\times 2^1+a_2\times 2^2+a_3\times 2^3+{a_4\times 2^4}\\ [A]_真= \begin{cases} a_0\times 2^0+a_1\times 2^1+a_2\times 2^2+a_3\times 2^3+{a_4\times 2^4} \color{red}{-2^5} & \text{if} & a_4=1\\ a_0\times 2^0+a_1\times 2^1+a_2\times 2^2+a_3\times 2^3+{a_4\times 2^4} & \text{other.} & (a_4=0) \end{cases}

分类讨论一下代入

[A]真={a0×20+a1×21+a2×22+a3×23+1×24−25ifa4=1a0×20+a1×21+a2×22+a3×23+0×24other.(a4=0)[A]_真=\begin{cases} a_0\times 2^0+a_1\times 2^1+a_2\times 2^2+a_3\times 2^3+{\color{blue}{1}\times 2^4} \color{red}{-2^5} & \text{if} & a_4=1\\ a_0\times 2^0+a_1\times 2^1+a_2\times 2^2+a_3\times 2^3+{\color{blue}{0}\times 2^4} & \text{other.} & (a_4=0) \end{cases}

化简：

[A]真={a0×20+a1×21+a2×22+a3×23+(−1)×24ifa4=1a0×20+a1×21+a2×22+a3×23+0×24other.(a4=0)[A]_真=\begin{cases} a_0\times 2^0+a_1\times 2^1+a_2\times 2^2+a_3\times 2^3+{\color{blue}{(-1)}\times 2^4} & \text{if} & a_4=1\\ a_0\times 2^0+a_1\times 2^1+a_2\times 2^2+a_3\times 2^3+{\color{blue}{0}\times 2^4} & \text{other.} & (a_4=0) \end{cases}

那我们可以看出来，a4a_4可以直接当成负权了，即：

[A]真=a0×20+a1×21+a2×22+a3×23+a4×(−24)[A]_真=a_0\times 2^0+a_1\times 2^1+a_2\times 2^2+a_3\times 2^3+\color{blue}{a_4\times(-2^4) }

把符号位用括号括起来。可以进行直接带负权的补码乘法。

例：用直接补码计算 x=11011x=11011 和 y=−11111y=-11111 的乘积。

image-20240916225017139